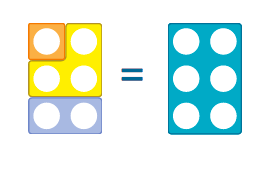Digit Dog

Calculating, Christmas, Number sense, Numicon

Christmas Challenge – Day 2

Posted on December 2, 2018January 8, 2019 by Digit Dog

Two Numicon® shapes – which shapes are in the Christmas sack?

Screenshot 2018-11-30 18.20.20

Show me 2 shapes that could be in the sack. Why do you think that? Are you sure? Convince me.

Are they the only 2 shapes it could be?

How many pairs could it be?

If I show you one of the shapes will you know for sure what the other one is?

Encourage children to explain their reasoning. At first, why don’t they know for sure which two shapes are in the sack? How many possible pairs can it be? Show one pair, and another, and another………..

When you know one shape, how can you be sure what the other shape is?

Variations

Put one shape in the sack and give children clues so that they can work out which shape it is. An opportunity to model mathematical language. My shape is:
- one more / one less than………
- two more/ two less than………
- in between……
- an odd/even number
- If I add …and …..I get this number
- If I take my number away from 10, I am left with……
- The difference between my number and 6 is………
- ……more than……
- a multiple of ……….
- a factor of………Get the children to ask questions about your shape to work out which one it is.
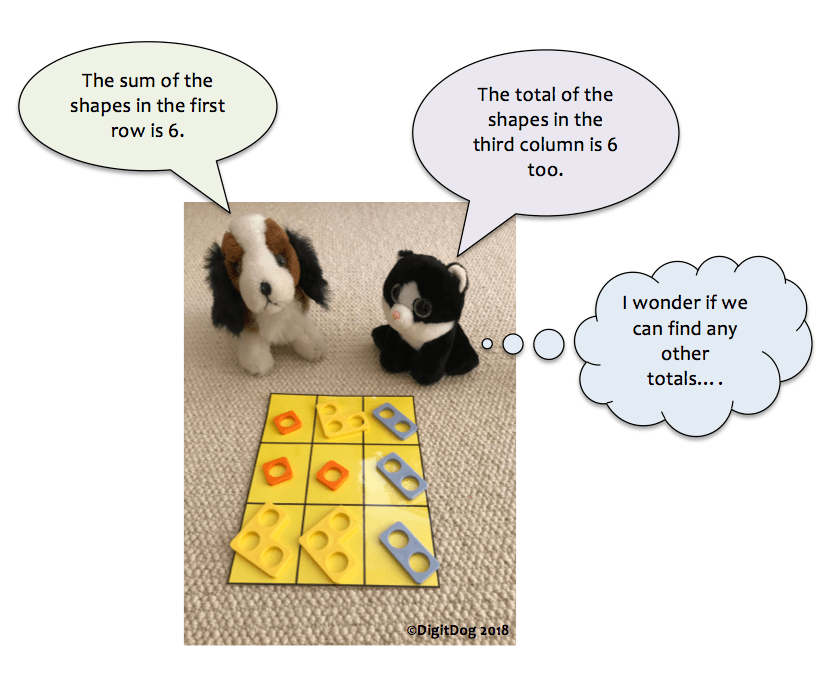
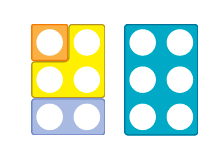
Put 3 shapes in the sack. The total is 15 which shapes could they be? What if I show you 1 shape, how does that change your thinking?
Vary the totals, vary the number of shapes.

Christmas, Numicon, Problem solving

Christmas Challenge Day 1

Posted on December 1, 2018January 8, 2019 by Digit Dog

One Santa’s sleigh – put the presents on Santa’s sleigh

You will need Santa’s sleighs (download and print) and a set of Numicon® shapes. Match the shapes to the spaces on the sleigh.

Screenshot 2018-11-30 16.27.13

Give children just the shapes they need and let them match them to the spaces on the sleigh.
Have a complete set of shapes for children to choose from.
When the sleigh is covered, one partner closes their eyes, the other takes away one shape. Which one is missing?
For an extra challenge, put the shapes in a feely bag and find the ones you need by touch alone.

Ask:

How many shapes do you need?

Which shape will fit here…..?

Is the shape that goes here big or small? Bigger / smaller than a red one?

Can you take away one shape and put two in its place?

Which shapes are easy to find?

5. Start with the blank sleigh and ask learners to use the Numicon shapes to cover it in any way they can.

How many different ways can you do it? Compare your sleigh with your friend’s. What’s the same and what’s different?

What if…………

You weren’t allowed to use the same shape more than once? How many ways can you do it? Is this more difficult? What are you thinking?

Can you use one shape repeatedly to cover the sleigh? Which shapes will work? Which won’t? Why?

What is the fewest number of shapes you can use? The most?

You use only odd shapes? Only even?

Find more ideas in the Santa’s Sleigh Challenge Booklet

Christmas, Numicon

Another Present Challenge

Posted on November 30, 2018January 8, 2019 by Digit Dog

Choose one of the presents, make multiple copies and challenge children to use 2 Numicon shapes to cover the space on it.

Use Digit Dog as a starting point:

Digit Dog and Calculating Cat have found 2 Numicon shapes to fit on their present.

I wonder how many different ways they can do it?

What do you notice?

How will they know if they have found all the ways? Explain your thinking.

Can you put the presents in order?

What if…….…

They used more than 2 shapes?

They tried one of the other presents?

Christmas, Numicon

Cover the Present – a Digit Dog challenge

Posted on November 28, 2018January 8, 2019 by Digit Dog

Digit Dog and Calculating Cat are trying to find the Numicon shape that fits on their presents.

Present Challenge 1

Spread out one set of presents (download here) and one set of Numicon shapes.

Ask: Which shape fits each present?

Which shapes are easy to find? Why?

Which are more difficult? Why?

For more of a challenge: Put the Numicon shapes in a feely bag. Choose one present, then feel in the bag to see if you can find the shape that fits it.

Ask children to reason about which shape could fit on each present:

What are you thinking?

Which shape do you think it will be?

Which shape can’t it be?

Is it bigger than the red shape? Is it smaller than the purple?

Which shapes are easy / hard to find?

Calculating, Making totals, Numicon

Total 6

Posted on September 26, 2018January 8, 2019 by Digit Dog

An extension of Investigating totals

Put the shapes on the grid but this time each row, column and diagonal has to have the same total.

6 grid

You might want to make the task simpler:

Make each row total 6
Make each column total 6
Make the rows and columns total 6
Include the diagonals.

Which shapes are you using in each row / column? Why?

Is there more than one way of completing the grid?

Look at your partner’s grid. What is the same and what is different?

Make the task more challenging:

Use digit cards instead of the shapes.
Don’t give the total – Can you put the Numicon shapes on the grid so that each row, column and diagonal add to the same total?

What do you think the total might be? Why?

How are you going to start? What are you going to try first?

What if.……..you used three different consecutive shapes?

3 twos, 3 threes and 3 fours 3 threes, 3 fours and 3 fives

Screenshot 2018-09-26 14.28.32 or Screenshot 2018-09-26 14.28.43

What will the totals of each row be now?

Screenshot 2018-09-26 15.51.01

Calculating, Making totals, Numicon

Investigating totals

Posted on September 23, 2018June 20, 2019 by Digit Dog

Digit Dog has got a 3 x 3 grid and 9 Numicon shapes – 3 one shapes, 3 two shapes and 3 three shapes. He is going to put the shapes on the grid and investigate the totals he can make.

Screenshot 2018-09-23 15.50.21

This is what he does first:

Screenshot 2018-09-23 15.50.32

Copy what Digit Dog has done.

Digit Dog says that the sum of the shapes in the first row is 6. Do you agree with Digit Dog? Why or why not? Are you sure?

Expecting learners to explain their thinking helps develop their reasoning skills.

If you agree, convince me that Digit Dog is correct. If you don’t agree, explain why you think he is wrong.

Encourage learners to explain why the total of the first row is 6. Use the Numicon shapes to show that the 3 shapes in the first row are equivalent to a six-shape. Explanations are much easier when you use concrete apparatus.

Screenshot 2018-09-23 18.01.53 Screenshot 2018-09-23 18.01.40

Screenshot 2018-09-23 18.07.13

Use the pan balance to explain.

Calculating Cat says that the total of the shapes in the third column is 6 too. Is she right? How do you know?

What is the same and what is different about Digit Dog’s row and Calculating Cat’s column?

Can you find any other rows or columns that total 6? Are there any that total more than 6? What about less than 6?

Can you find a row or column that totals 1 more than 6? What about 1 less than 6?

What else do you notice?

How are you going to record the totals you have found?

Now arrange the shapes on the grid in any way you want and investigate the totals that you make. What do you notice? What is the largest total you can make? The smallest total?

Look at a grid your friend has done. What is the same? What is different?

What if you used other shapes?

Problem solving

Ladybird Box

Posted on September 16, 2018January 8, 2019 by Digit Dog

Digit Dog saw the Ladybird Box problem on www.nrich.maths.org/144 and thought he’d try it out.

The Challenge

The box has 9 little square compartments. Can you put the 6 ladybirds in the box so that there are just 2 ladybirds in every column and every row?

Ladybird box

I wonder how many ways there are to do the puzzle?

Does it matter which compartment you put the first ladybird in?

What do you need to keep checking? Remember that each row and each column can only have 2 ladybirds in them.

How many empty compartments will there be?

Record your work on this grid

Look at your friend’s solution. What is the same? What is different?

WODB

Digit Dog is making his own “Which one doesn’t belong?”

Posted on September 13, 2018December 21, 2018 by Digit Dog

dice

What do you notice?

Do you agree with Calculating Cat? What does she mean by “a double”?

Can you think of reasons why each of the pairs of dice could not belong?

Choose each pair of dice in turn and think of reasons why it doesn’t belong. Can you think of more than one reason?

Put this picture on your challenge board and come back to it during the day. How many answers can you think of by the end of the day?

Can you make up a “which one doesn’t belong?” of your own?

Books, Shape, WODB

which one doesn’t belong? A Shapes Book by Christopher Danielson

Posted on September 12, 2018January 8, 2019 by Digit Dog

Really enjoying this book:

A great way to focus on the properties of shape and to start conversations and thinking. Each page has four shapes and the challenge is to find which one doesn’t belong. Any answer is acceptable as long as it is true. The important thing is to have a reason for your answer.

Can you find a reason why each of the shapes on the cover don’t belong?

How is the shape you have chosen different from the others?

What do you notice?

By doing this activity you are encouraging learners to notice similarities and differences, to use correct mathematical language, to reason and to explain their thinking.

The question on each page of the book “Which one doesn’t belong?” is the same but some pages are more challenging than others. They really make you think.

Find more ideas from this author at www.talkingmathwithyourkids.com

What's the same / different?

What’s the same? What’s different?

Posted on July 6, 2018December 21, 2018 by Digit Dog

Noticing similarities and differences is key to spotting patterns and reasoning mathematically.

Ask learners “What is the same?” “What is different?”

Explaining what you notice improves your mathematical language and thinking.

Bugs

Look at the two sets of bugs and find similarities and differences. Accept all answers. Encourage learners to keep looking for more. Make a list that can be added to during the day / week.

What can you say about the two groups of bugs? What do you notice?

Can you think of anything that is the same?

I can see that each group has 3 bugs. Each group has the same number of bugs.

Encourage and model the use of full sentences.

Anything else?

In each group, the bugs have different coloured eyes.

The number of spots on all the bugs in both groups is an even number.

If you add up the number of spots, in each group the total is more than 10 .

Both groups have two bugs with a double.

Can you think of more things that are the same?

What about the differences? What is different about the two groups?

I can see that one group has all green bugs and the other has different colours.